Vulkan ProRes decoder: optimization

Introduction

In two previous posts, focused on a GPU-based decoder for Apple Prores, I introduced the structure and decoding process of the codec, and decribed my initial implementation. In early August, roughly 2 months after the coding period started, I had reached feature completeness and the project was fairly robust, so it was time to move to optimization.
In this post, I will detail the steps my process and the steps I took, broken down between each shader, and finally present the results of this work.

Initial situation

TODO.

Entropy decoding (color/alpha)

This section is about the variable-length decoding (VLD) steps of the decoding process.

Getting rid of the slice context buffer

During the VLD step, the decoder needs to know the size and position of the slice it is processing. ProRes tiles picture into a regular grid, the size of which is determined by the log2_desired_slice_size_in_mb syntax element, whose value has to be inferior or equal to 3. It does so by horizontally filling the picture with as many slice of size 1 << log2_desired_slice_size_in_mb as possible. If space remains, it inserts a slice of the next possible power of two, and so on until the whole picture is covered (see Figure 1).

In the initial version of the decoder, a GPU buffer was filled from the CPU, containing position and size values for each slice. Each GPU thread would then index this buffer to figure out how many values to output, and where to write them.

⊕ Show captionFigure 1: ProRes slice tiling for a 336 px-wide picture, with log2_desired_slice_size_in_mb = 3.
The space is divided in 4 slices, 2 “full” (of size 8 Mbs) and 2 “extras” (of size 4 and 1 MBs).

The advantages of calculating the values in-shader, and removing this buffer are two-fold:

• Decrease memory usage. Since each slice context element was 4 bytes big (including padding), for a 4k-resolution video containing over 4000 slices, this amounted to around 16 kib per frame. Moreover, the decoder supports multithreading and will push command buffers from (usually) as many threads as CPU cores, each using a separate slice context buffer retrieved from a pool.
• Decrease PCI traffic. The slice positions and sizes were calculated on the CPU, and written to a memory-mapped, device-local buffer. Additionally, this also decreases VRAM and L2 cache usage, leaving room for other data.

So we need an expression to derive the slice attributes from the following parameters: slice id (slice_id), size of the picture in MBs (mb_width), size of the picture in slices (slice_width).
The first observation is that the mb_width parameter also represents the number of full slices, when interpreted as fixed-point with log2_desired_slice_size_in_mb fractional bits . The immediate consequence is that we can derive the number of “full” and “extra” slices from it, the latter by counting the number of bits in the fractional part of the value,This can be efficiently implemented in GLSL by using bitfieldExtract and bitCount. These two built-ins directly map to hardware instructions on NVidia (SGXT and POPC) and AMD (s_bfe_u32 and s_bcnt1_i32_b32). and the former by substracting this from slice_width (see Figure 2).
Secondly, we note that the size of the $n$-th extra slice is given by the exponentiation of two by the $n$-th bit most significant in the fractional part of mb_width. We denote the position of this bit with extra_bit. The slice size can therefore be calculated as:

• 1 << log2_desired_slice_size_in_mb for a full slice;
• 1 << extra_bit for an extra slice.

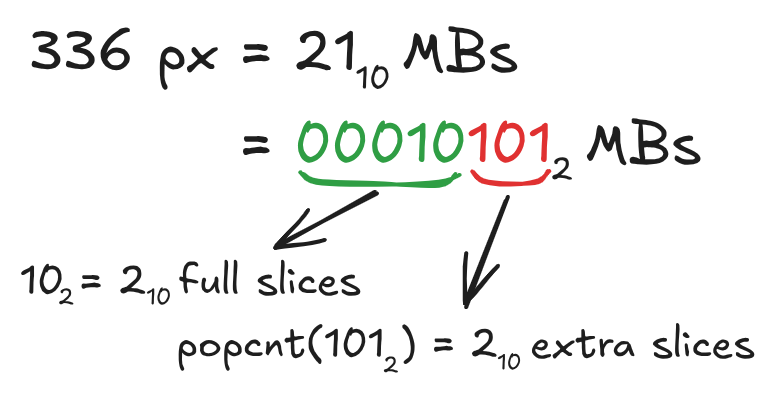⊕ Show captionFigure 2: Visualization of the fixed-width fractional representation of mb_width, using the structure in Figure 1 as example.

How to efficiently compute extra_bit? At first, I found that the CUDA intrinsic __fns does exactly what we need,The expression would be __fns(mb_width, log2_desired_slice_size_in_mb, -slice_id). and seemed like a promising lead. However, investigating the produced SASS, I found that this built-in does not map to hardware instruction, and instead generates a sizeable amount of code, including branches and loops (see godbolt).Funnily enough, the ROCm compiler is able to optimize certain cases with hardcoded bit parameters better than nvcc (see godbolt).
My idea was then to right-shift mb_width by diff = slice_width - slice_id - 1 to clear the low bits, use findLSB to get the position of extra_bit, and finally add back diff to compensate for the shift. This works fine for most cases but breaks down for the fractional bit pattern 0b110, evaluating to findLSB(0b110 >> 0) + 0 = 1 (correct) and findLSB(0b110 >> 1) + 1 = 2 (incorrect).
I solved this by substracting diff from mb_width before the right-shift, which flips the bit before our target to 0. This actually works, but sort of by accident, as the expression does not generalize as a generic way find the $n$-th set bit in a pattern longer than 3 bits.Finding a counter-example for a 4-bit pattern is trivial. Verification of this expression can be done simply by exhaustive checking, as shown below:

We then need a way to compute the macroblock position of the slice within the overall picture. Following a similar reasoning, we notice that the position is the number of “full” slice left-shited by log2_desired_slice_size_in_mb, plus the fractional part of mb_width, with bits taken above and excluding extra_bit. These bits can be extracted by constructing an appropriate mask, and we do so using 0xf << (extra_bit + 1). With this, the slice context buffer can be completely eliminated.

Finally, we can eliminate the branching described above for the calculation of the slice size, by appropriate use of min/max. While these operations are commonly not considered branchless, GPU architectures have dedicated, un-predicated instructions for them (IMNMX on NVidia, s_{min,max}_u32 on AMD), so I will consider it good enough.

The final expressions looks like this, where log2_width is the log2 of the slice with in MBs, and mb_pos its position in MBs within the picture. The off variable is an offset added to the expression derived above, that allows the min to work by being superior to log2_desired_slice_size_in_mb if the slice is a “full” one, and 0 otherwise.

uint frac      = bitfieldExtract(uint(mb_width), 0, log2_desired_slice_size_in_mb),
     num_extra = bitCount(frac);

uint diff = slice_width - slice_id - 1,
     off  = max(int(diff - num_extra + 1) << 2, 0);

uint log2_width = min(findLSB(frac - diff >> diff) + diff + off, log2_desired_slice_size_in_mb);

uint mb_pos = (min(slice_id, slice_width - num_extra) << log2_desired_slice_size_in_mb) +
              (frac & (0xf << log2_width + 1));

Inverse transform

This section is about the IDCT step of the decoding process.

NVidia IDCT

TODO.

AAN IDCT

TODO.

Using packed FP16 math

TODO.

Using subgroup operations

TODO?

Using cooperative matrices

TODO.